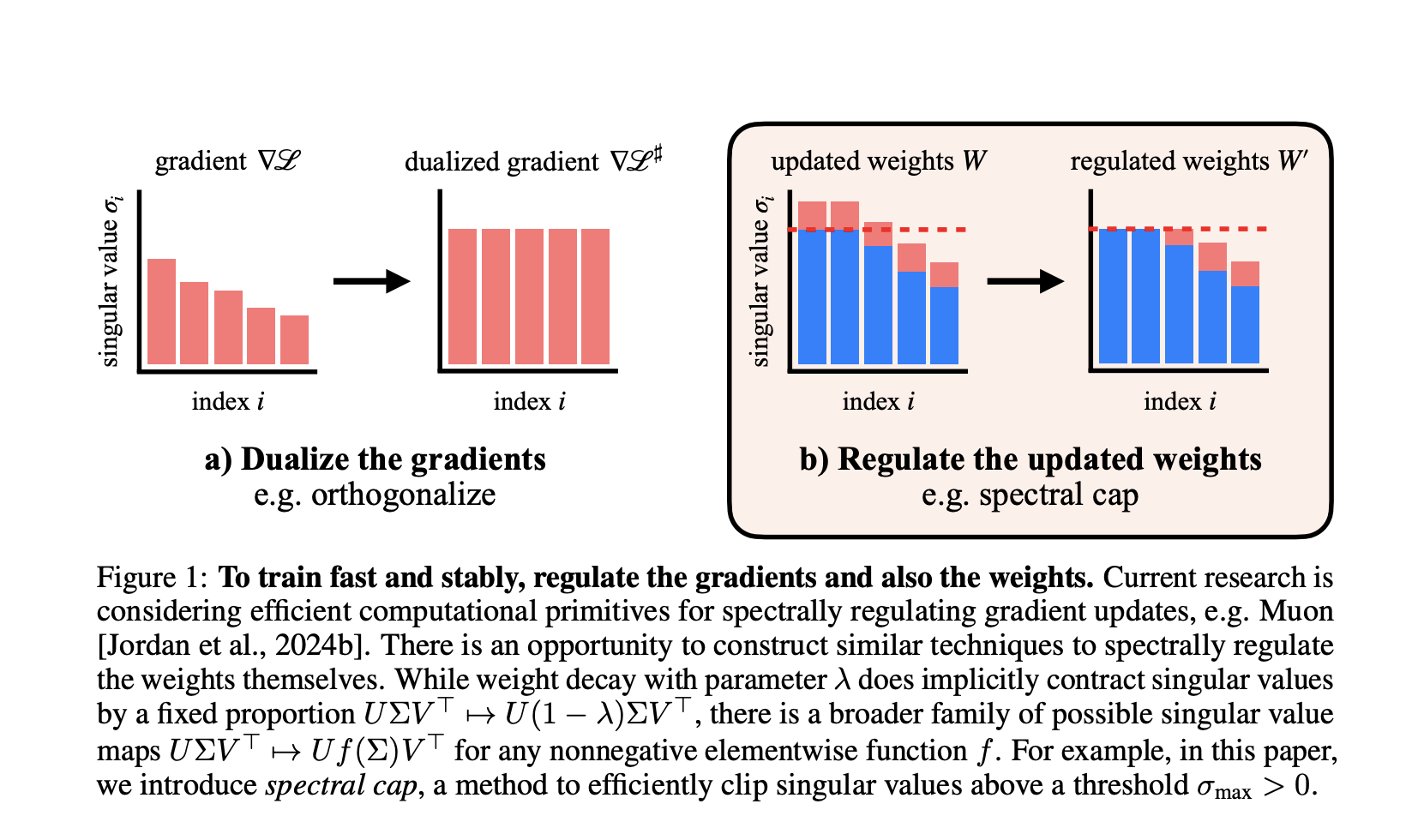
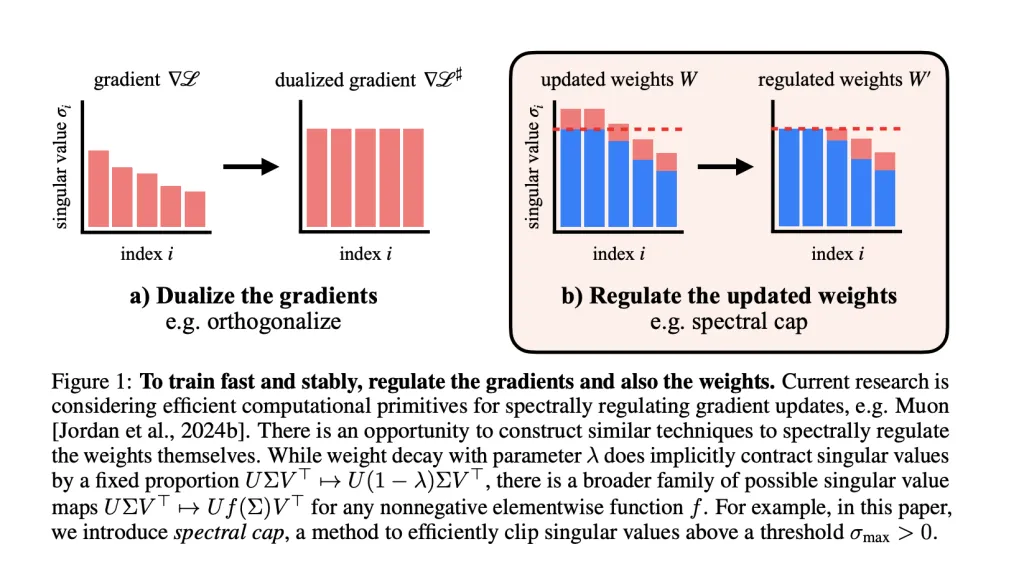
Coaching large-scale transformers stably has been a longstanding problem in deep studying, notably as fashions develop in measurement and expressivity. MIT researchers deal with a persistent drawback at its root: the unstable development of activations and loss spikes attributable to unconstrained weight and activation norms. Their answer is to implement provable Lipschitz bounds on the transformer by *spectrally regulating the weights—*with no use of activation normalization, QK norm, or logit softcapping tips.
What’s a Lipschitz Sure—and Why Implement It?
A Lipschitz certain on a neural community quantifies the utmost quantity by which the output can change in response to enter (or weight) perturbations. Mathematically, a operate fff is KKK-Lipschitz if:∥f(x1)−f(x2)∥≤Ok∥x1−x2∥ ∀x1,x2|f(x_1) – f(x_2)| leq Ok |x_1 – x_2| forall x_1, x_2∥f(x1)−f(x2)∥≤Ok∥x1−x2∥ ∀x1,x2
- Decrease Lipschitz certain ⇒ better robustness and predictability.
- It’s essential for stability, adversarial robustness, privateness, and generalization, with decrease bounds which means the community is much less delicate to adjustments or adversarial noise.
Motivation and Drawback Assertion
Historically, coaching secure transformers at scale has concerned a wide range of “band-aid” stabilization tips:
- Layer normalization
- QK normalization
- Logit tanh softcapping
However these don’t straight tackle the underlying spectral norm (largest singular worth) development within the weights, a root reason for exploding activations and coaching instability—particularly in massive fashions.
The central speculation: If we spectrally regulate the weights themselves—past simply the optimizer or activations—we will keep tight management over Lipschitzness, probably fixing instability at its supply.
Key Improvements
Weight Spectral Regulation and the Muon Optimizer
- Muon optimizer spectrally regularizes gradients, guaranteeing every gradient step doesn’t improve the spectral norm past a set restrict.
- The researchers prolong regulation to the weights: After every step, they apply operations to cap the singular values of each weight matrix. Activation norms keep remarkably small because of this—not often exceeding values appropriate with fp8 precision of their GPT-2 scale transformers.
Eradicating Stability Methods
In all experiments, no layer normalization, no QK norm, no logit tanh have been used. But,
- Most activation entries in their GPT-2 scale transformer by no means exceeded ~100, whereas the unconstrained baseline surpassed 148,000.
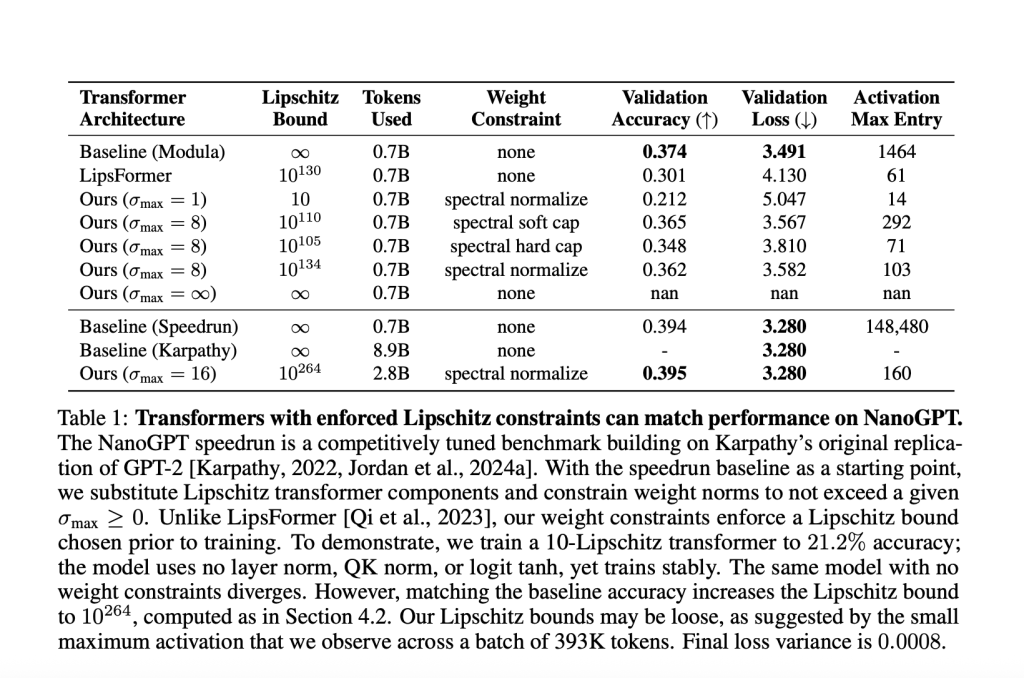
Desk Pattern (NanoGPT Experiment)
| Mannequin | Max Activation | Layer Stability Methods | Validation Accuracy | Lipschitz Sure |
|---|---|---|---|---|
| Baseline (Speedrun) | 148,480 | Sure | 39.4% | ∞ |
| Lipschitz Transformer | 160 | None | 39.5% | 10¹⁰²⁶⁴ |
Strategies for Imposing Lipschitz Constraints
A wide range of weight norm constraint strategies have been explored and in contrast for his or her means to:
- Preserve excessive efficiency,
- Assure a Lipschitz certain, and
- Optimize the performance-Lipschitz tradeoff.
Strategies
- Weight Decay: Normal methodology, however not all the time strict on spectral norm.
- Spectral Normalization: Ensures high singular worth is capped, however could have an effect on all singular values globally.
- Spectral Tender Cap: Novel methodology, easily and effectively applies σ→min(σmax,σ)sigma to min(sigma_{textual content{max}}, sigma)σ→min(σmax,σ) to all singular values in parallel (utilizing odd polynomial approximations). That is co-designed for Muon’s excessive stable-rank updates for tight bounds.
- Spectral Hammer: Units solely the biggest singular worth to σmaxsigma_{textual content{max}}σmax, finest fitted to AdamW optimizer.
Experimental Outcomes and Insights
Mannequin Analysis at Numerous Scales
- Shakespeare (Small Transformer, <2-Lipschitz):
- Achieves 60% validation accuracy with a provable Lipschitz certain under.
- Outperforms unconstrained baseline in validation loss.
- NanoGPT (145M Parameters):
- With a Lipschitz certain <10, validation accuracy: 21.2%.
- To match the sturdy unconstrained baseline (39.4% accuracy), required a big higher certain of 1026410^{264}10264. This highlights how strict Lipschitz constraints typically commerce off with expressivity at massive scales for now.
Weight Constraint Technique Effectivity
- Muon + Spectral Cap: Leads the tradeoff frontier—decrease Lipschitz constants for matched or higher validation loss in comparison with AdamW + weight decay.
- Spectral mushy cap and normalization (below Muon) persistently allow finest frontier on the loss-Lipschitz tradeoff.
Stability and Robustness
- Adversarial robustness will increase sharply at decrease Lipschitz bounds.
- In experiments, fashions with a constrained Lipschitz fixed suffered a lot milder accuracy drop below adversarial assault in comparison with unconstrained baselines.
Activation Magnitudes
- With spectral weight regulation: Most activations stay tiny (near-fp8 appropriate), in comparison with the unbounded baselines, even at scale.
- This opens avenues for low-precision coaching and inference in {hardware}, the place smaller activations scale back compute, reminiscence, and energy prices.
Limitations and Open Questions
- Deciding on the “tightest” tradeoff for weight norms, logit scaling, and a focus scaling nonetheless depends on sweeps, not precept.
- Present upper-bounding is unfastened: Calculated world bounds might be astronomically massive (e.g. 1026410^{264}10264), whereas actual activation norms stay small.
- It’s unclear if matching unconstrained baseline efficiency with strictly small Lipschitz bounds is feasible as scale will increase—extra analysis wanted.
Conclusion
Spectral weight regulation—particularly when paired with the Muon optimizer—can stably practice massive transformers with enforced Lipschitz bounds, with out activation normalization or different band-aid tips. This addresses instability at a deeper stage and retains activations in a compact, predictable vary, tremendously enhancing adversarial robustness and probably {hardware} effectivity.
This line of labor factors to new, environment friendly computational primitives for neural community regulation, with broad purposes for privateness, security, and low-precision AI deployment.
Take a look at the Paper, GitHub Web page and Hugging Face Venture Web page. Be happy to take a look at our GitHub Web page for Tutorials, Codes and Notebooks. Additionally, be happy to observe us on Twitter and don’t overlook to affix our 100k+ ML SubReddit and Subscribe to our E-newsletter.
Sana Hassan, a consulting intern at Marktechpost and dual-degree scholar at IIT Madras, is enthusiastic about making use of know-how and AI to handle real-world challenges. With a eager curiosity in fixing sensible issues, he brings a recent perspective to the intersection of AI and real-life options.